連載
本日の1杯 vol.23【北欧のインテリアに囲まれながらシングルモルトを嗜む】:bar nems
誰しもひとりでじっくり飲みたいときもある。いつも行っているバーだと、顔なじみの常連たちがいるので、行き先に悩んでしまう。そんな時に足を向けたい、隠れ家的な「bar nems(ネムス)」だ。4年ほど前に...
「12月に入ると『今日は討ち入りだ』であるとか、『今日は真珠湾だな』などとつい言ってしまう」こんなジョークの通り、12月には印象深い「○○の日」が多くある。いま記した討ち入り…&hell...
【第41回】旅路編 ついに来た!?「部長と行く魅惑の台湾2泊3日旅」初日
←第40回へ旅ふぇち旅バカ旅命!おしゃれパッカー部長(部員約1名)、はし袋やら買い物袋やら看板をかなぐり捨てて、ついに私らを台湾添乗でございます。もう行っちゃお、ってことですな部長!さあまず...
テレビを点けてみると本当に多種多様、様々な番組が放送されていると感心するが、これが休日ともなると、ジャンルが「趣味」となりそうな番組がこれでもかと並んでいる。多趣味を自認する人は、日曜の朝から将棋&r...
【第40回】旅情編 「なんなのでしょーか。」って、ちょっと部長!
←第39回へ旅ふぇち旅バカ旅命!おしゃれパッカー部長(部員約1名)、もうこうなったらまとめて出しちゃえ的な攻撃に打って出られました。なんというんでしょう、シュールって言うんですよね、やっぱり...
早いもので来週からは12月。あっという間に新年はやってきますよと迫られているが如く、年賀状の発売なども始まっているが、今回はそんな年賀状を運んでくれる郵便ポストのおはなしを。こちらが海底郵便ポスト。現...
ただいま現在私ども「あそびすと編集部」では、我らがアラカン編集長がモンブランについに登ってしまった(笑)ことを受けて、その道中記たる電子書籍の製作が急ピッチに行なわれている。早くみなさまの目に留まるよ...
←第38回へ 旅ふぇち旅バカ旅命! おしゃれパッカー部長(部員約1名)、 美味しいものに続きまして、今回は看板なおはなし。 いやあ、すごいですねえ、単純に(笑)。 下のほうの救急車もすごい...
本日の1杯 vol.22【ソーダでアップする濃いめのモスコミュール】:XANADU
「本日は女性とデート」てな向きには、葉巻が置いてあるシックなオーセンティックより、少しおしゃれなバーはいかがか。「Shot Bar XANADU(ザナドゥ)」。JR五反田駅から200mほど歩いた桜田通...
江戸幕府末期の御用金360万両が群馬県の赤城山麓に埋蔵されている――。この伝説の埋蔵金発掘を狙って大々的に赤城山麓を掘り返したテレビ番組がいまとなっては懐かしい。田中信夫の「いま開かれる、黄金の扉っ」...
←第37回へ旅ふぇち旅バカ旅命!おしゃれパッカー部長(部員約1名)、前回が台湾北部の美味しいものでしたので、当然今回は南部でございます。再登場のマンゴーかき氷を筆頭に、シチュー入りからお好み...
先日のこと。深夜のコンビニエンスストアでおつりを受け取り、翌朝その500円玉を確認したところ、思わずこんな声が出た。「うわっ、ニセガネだっ」いや、よくよく見てみると、09年に発行された今上天皇在位20...
←第36回へ旅ふぇち旅バカ旅命!おしゃれパッカー部長(部員約1名)、今回は台湾中の名物ごはん、北地方編でございます。いやあ、美味しそうなものというのは写真だけでも罪ですな。「おいしい」ってひ...
去る23日、JRA(日本中央競馬会)京都競馬場で行なわれた第72回菊花賞でオルフェーヴル号が優勝。オルフェーヴルは春の二冠も制していたことから、有史からの中央競馬史上7頭目の三冠馬の栄誉に輝いた。毎年...
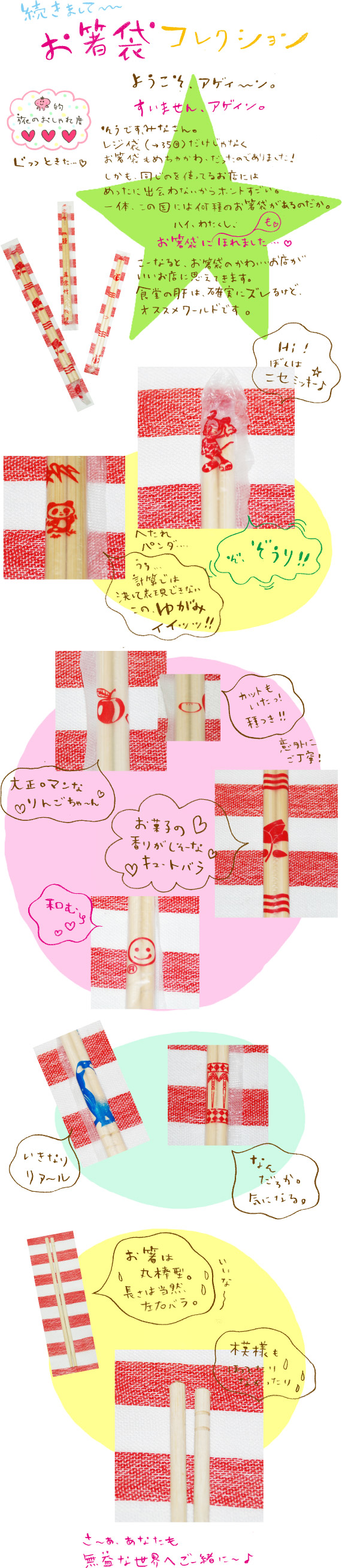
【第36回】旅情編 「台北の、心のおはしス、箸袋」(とまこ芭蕉)
←第35回へ旅ふぇち旅バカ旅命!おしゃれパッカー部長(部員約1名)、中国出張から帰ってきての一発目は……箸袋。前回のレジ袋に続く部長ワールドですねえ。しかしよく見...
本年の日本プロ野球(NPB)、パシフィック・リーグ(パ・リーグ)は福岡ソフトバンクホークスがブッちぎりで優勝。方やセントラル・リーグ(セ・リーグ)は逃げる東京ヤクルトスワローズを中日ドラゴンズが大逆転...
終わりは始まりの始まり!! 9月2日にスイスから帰国して早やひと月半が経った。「モンブランに登ろう」と思い始めて3年越し。思い詰めて、ついに叶った登頂。そりゃあ、大はしゃぎ、嬉しかった。大感動だよね...
1年以上前に3回取り上げた「アレの名前」が今回のテーマである。よく目にはするものの、そういえば正式な名前をよく知らない、そんな存在をご紹介する。ちなみに以前の3回は「ソラリー」、「ランドルト環」、「踊...
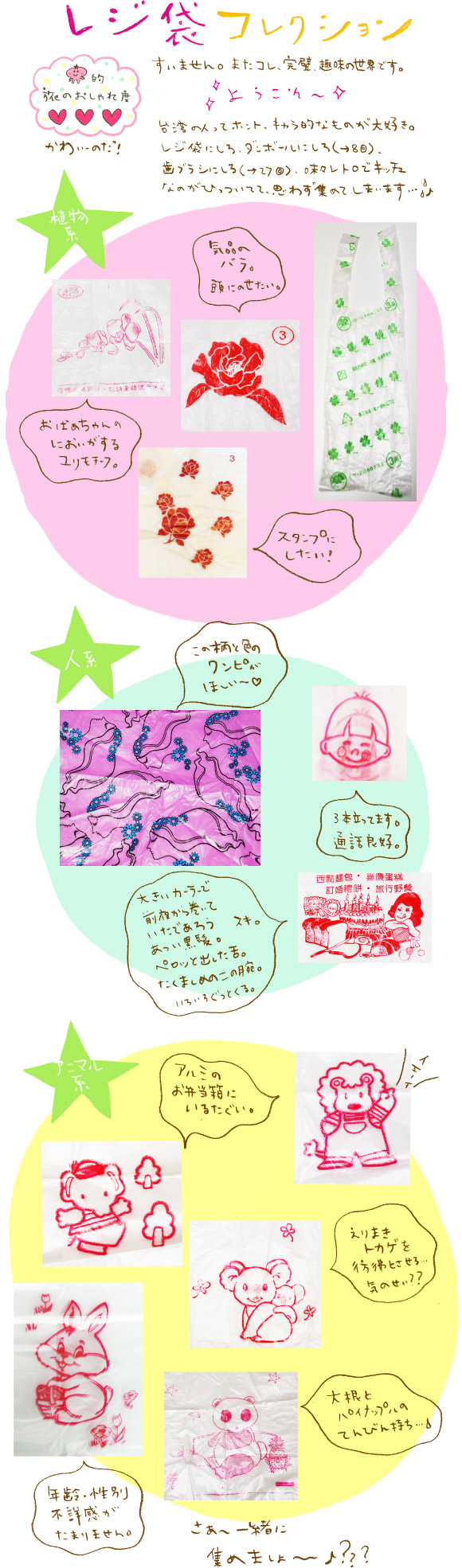
←第34回へ 旅ふぇち旅バカ旅命! おしゃれパッカー部長(部員約1名)、 今回はまたこれ、レジ袋ですか。 部長の手にかかれば台湾はなんでもネタになりますねえ。 それはともかく、たしかに手間...
底辺×高さ÷2この式で求められるのは三角形の面積である。ではこの式で求められるものは何か?円周÷直径これ、もっとも簡単な「円周率」を求める式である。円周率の最初...